null - 程序员宅基地

如何理解最小二乘法？-程序员宅基地

最小平方法是十九世纪统计学的主题曲。从许多方面来看, 它之于统计学就相当于十八世纪的微积分之于数学。
----乔治·斯蒂格勒的《The History of Statistics》

1 日用而不知

来看一个生活中的例子。比如说，有五把尺子：

用它们来分别测量一线段的长度，得到的数值分别为（颜色指不同的尺子）：

$\begin{array}{c|c} \qquad\qquad&\qquad长度\qquad\\\hline \color{red}红& 10.2 \\\hline \color{blue}蓝& 10.3 \\\hline \color{orange}橙&9.8\\\hline \color{Goldenrod}黄&9.9\\\hline \color{green}绿&9.8\\\end{array}$

之所以出现不同的值可能因为：

不同厂家的尺子的生产精度不同
尺子材质不同，热胀冷缩不一样
测量的时候心情起伏不定
......

总之就是有误差，这种情况下，一般取平均值来作为线段的长度：

$\overline{x}=\frac{10.2+10.3+9.8+9.9+9.8}{5}=10$

日常中就是这么使用的。可是作为很事'er的数学爱好者，自然要想下：

这样做有道理吗？
用调和平均数行不行？
用中位数行不行？
用几何平均数行不行？

2 最小二乘法

换一种思路来思考刚才的问题。

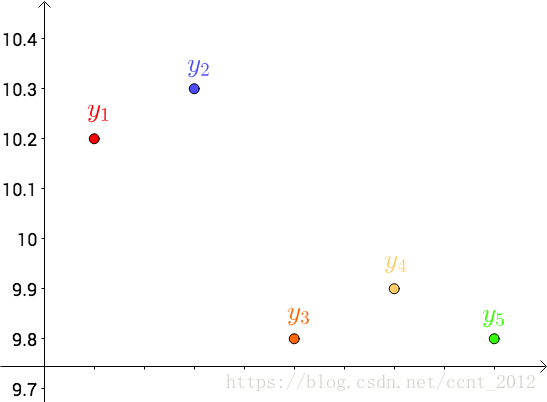
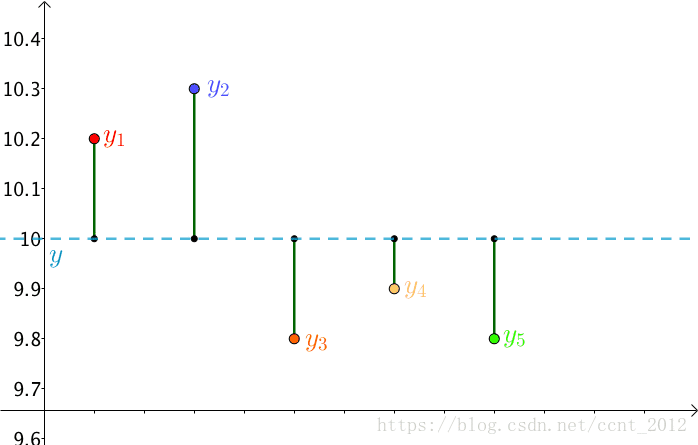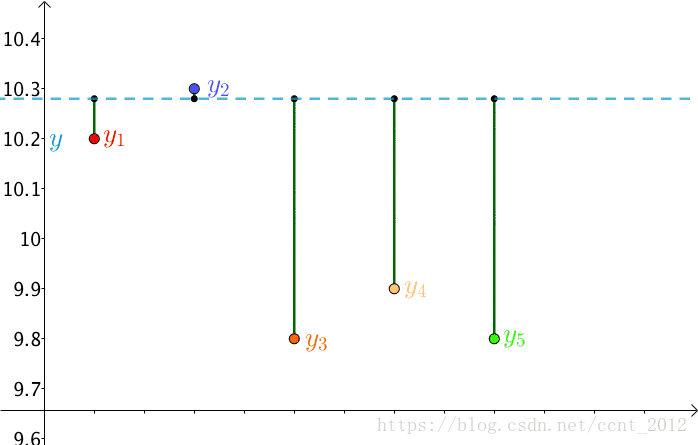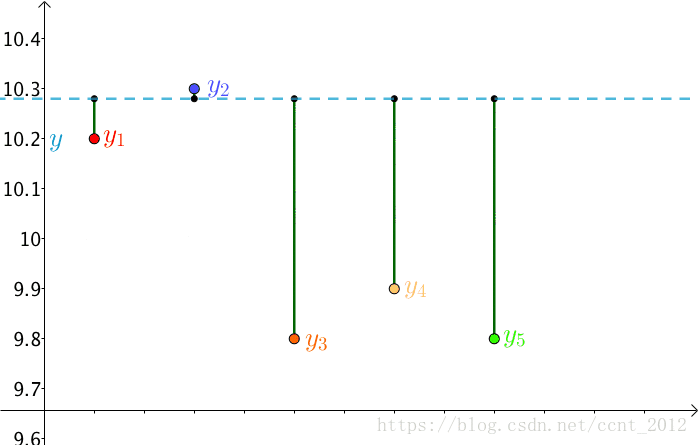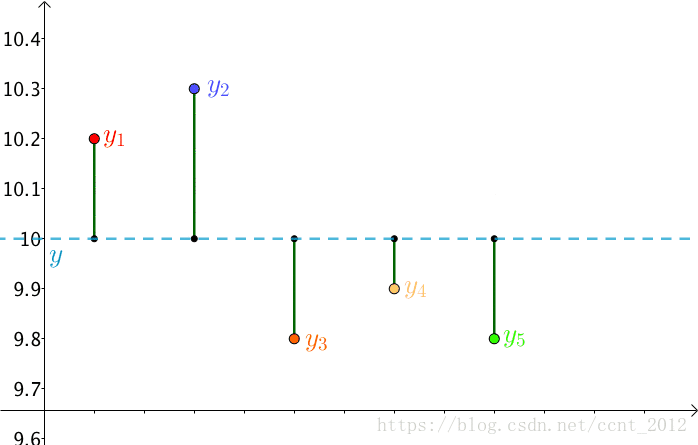
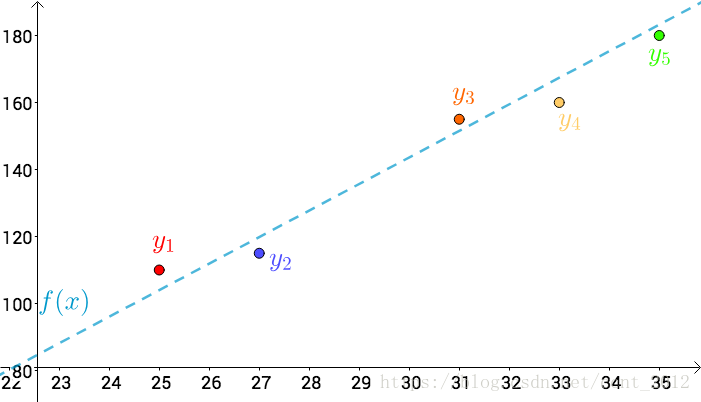
首先，把测试得到的值画在笛卡尔坐标系中，分别记作 $y_i$ ：

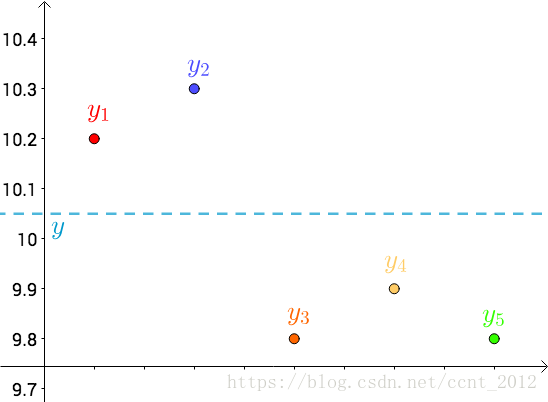
其次，把要猜测的线段长度的真实值用平行于横轴的直线来表示（因为是猜测的，所以用虚线来画），记作 $y$ ：

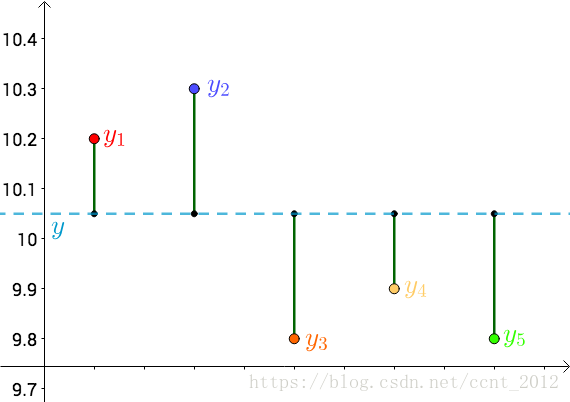
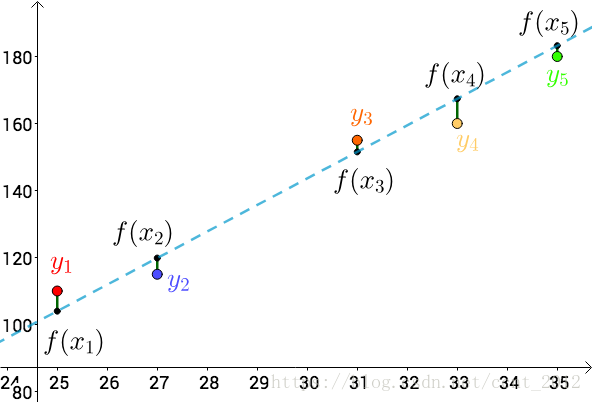
每个点都向 $y$ 做垂线，垂线的长度就是 $|y-y_i|$ ，也可以理解为测量值和真实值之间的误差：

因为误差是长度，还要取绝对值，计算起来麻烦，就干脆用平方来代表误差：

$|y-y_i|\to (y-y_i)^2$

总的误差的平方就是：

$\epsilon=\sum (y-y_i)^2$

因为 $y$ 是猜测的，所以可以不断变换：

自然，总的误差 $\epsilon$ 也是在不断变化的。

法国数学家，阿德里安-馬里·勒讓德（1752－1833，这个头像有点抽象）提出让总的误差的平方最小的 $y$ 就是真值，这是基于，如果误差是随机的，应该围绕真值上下波动（关于这点可以看下“如何理解无偏估计？”）。

这就是最小二乘法，即：

$\epsilon=\sum (y-y_i)^2最小\implies 真值y$

这个猜想也蛮符合直觉的，来算一下。

这是一个二次函数，对其求导，导数为0的时候取得最小值：

$\begin{aligned} \frac{d}{dy}\epsilon &=\frac{d}{dy}\sum (y-y_i)^2=2\sum (y-y_i)\\ \quad\\ &=2((y-y_1)+(y-y_2)+(y-y_3)+(y-y_4)+(y-y_5))=0 \quad\\\end{aligned}$

进而：

$5y=y_1+y_2+y_3+y_4+y_5\implies y=\frac{y_1+y_2+y_3+y_4+y_5}{5}$

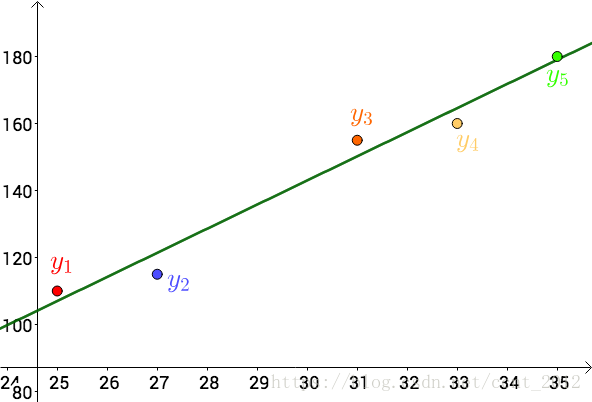
正好是算术平均数。

原来算术平均数可以让误差最小啊，这下看来选用它显得讲道理了。

以下这种方法：

$\epsilon=\sum (y-y_i)^2最小\implies 真值y$

就是最小二乘法，所谓“二乘”就是平方的意思，台湾直接翻译为最小平方法。

3 推广

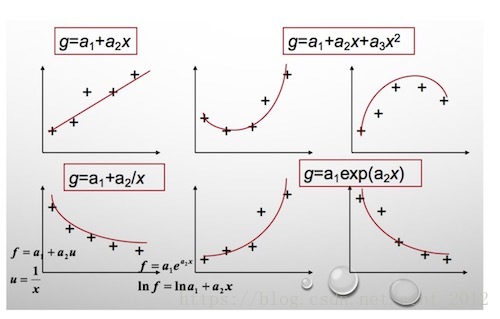
算术平均数只是最小二乘法的特例，适用范围比较狭窄。而最小二乘法用途就广泛。

比如温度与冰淇淋的销量：

$\begin{array}{c|c} \qquad\qquad&\qquad销量\qquad\\\hline \color{red}{25^\circ}& 110 \\\hline \color{blue}{27^\circ}& 115 \\\hline \color{orange}{31^\circ}&155\\\hline \color{Goldenrod}{33^\circ}&160\\\hline \color{green}{35^\circ}&180\\\end{array}$

看上去像是某种线性关系：

可以假设这种线性关系为：

$f(x)=ax+b$

通过最小二乘法的思想：

上图的 $i,x,y$ 分别为：

$\begin{array}{c|c|c} \qquad i\qquad&\qquad x\qquad&\qquad y\qquad\\\hline 1&25& 110 \\\hline 2&27& 115 \\\hline 3&31&155\\\hline 4&33&160\\\hline 5&35&180\\\end{array}$

总误差的平方为：

$\epsilon=\sum (f(x_i)-y_i)^2=\sum (ax_i+b-y_i)^2$

不同的 $a,b$ 会导致不同的 $\epsilon$ ，根据多元微积分的知识，当：

$\begin{cases} \frac{\partial}{\partial a}\epsilon=2\sum (ax_i+b-y_i)x_i=0\\ \quad\\ \frac{\partial}{\partial b}\epsilon=2\sum (ax_i+b-y_i)=0\end{cases}$

这个时候 $\epsilon$ 取最小值。

对于 $a,b$ 而言，上述方程组为线性方程组，用之前的数据解出来：

$\begin{cases} a\approx 7.2\\ \quad\\ b\approx -73\end{cases}$

也就是这根直线：

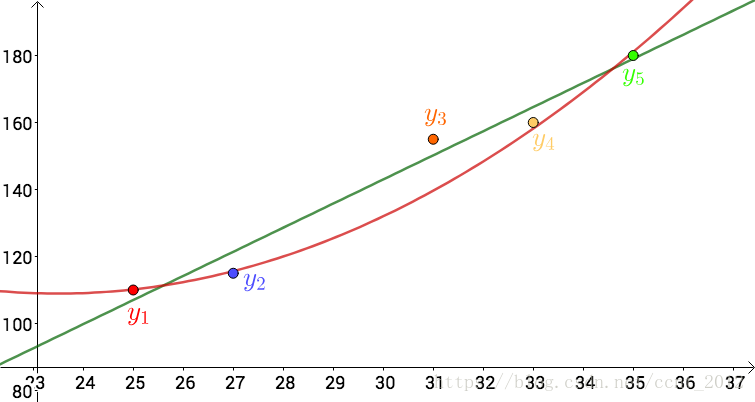
其实，还可以假设：

$f(x)=ax^2+bx+c$

在这个假设下，可以根据最小二乘法，算出 $a,b,c$ ，得到下面这根红色的二次曲线：

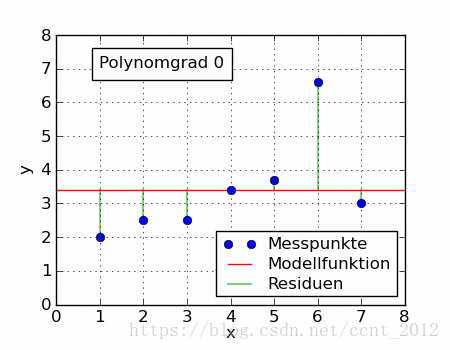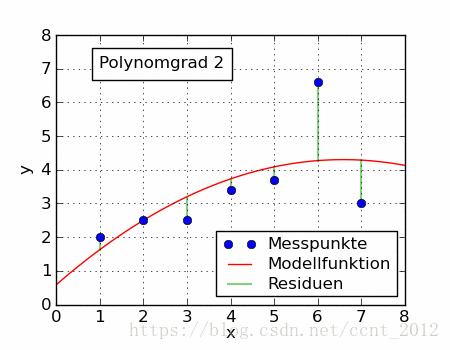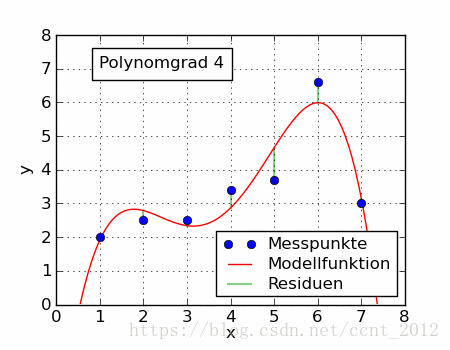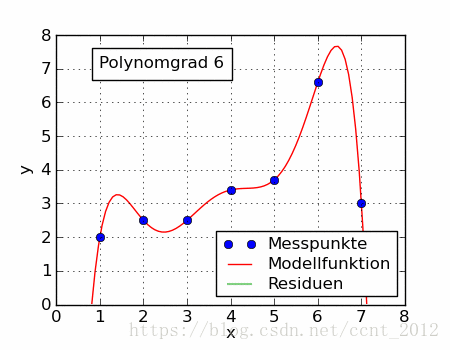
同一组数据，选择不同的 $f(x)$ ，通过最小二乘法可以得到不一样的拟合曲线（出处）：

不同的数据，更可以选择不同的 $f(x)$ ，通过最小二乘法可以得到不一样的拟合曲线：

$f(x)$ 也不能选择任意的函数，还是有一些讲究的，这里就不介绍了。

4 最小二乘法与正态分布

我们对勒让德的猜测，即最小二乘法，仍然抱有怀疑，万一这个猜测是错误的怎么办？

数学王子高斯（1777－1855）也像我们一样心存怀疑。

高斯换了一个思考框架，通过概率统计那一套来思考。

让我们回到最初测量线段长度的问题。高斯想，通过测量得到了这些值：

每次的测量值 $x_i$ 都和线段长度的真值 $x$ 之间存在一个误差：

$\epsilon_i=x-x_i$

这些误差最终会形成一个概率分布，只是现在不知道误差的概率分布是什么。假设概率密度函数为：

$p(\epsilon)$

再假设一个联合概率密度函数，这样方便把所有的测量数据利用起来：

$\begin{aligned} L(x) &=p(\epsilon_1)p(\epsilon_2)\cdots p(\epsilon_5)\\ \quad\\ &=p(x-x_i)p(x-x_2)\cdots p(x-x_5)\end{aligned}$

讲到这里，有些同学可能已经看出来了上面似然函数了（关于似然函数以及马上要讲到的极大似然估计，可以参考“如何理解极大似然估计法？”）。

因为 $L(x)$ 是关于 $x$ 的函数，并且也是一个概率密度函数（下面分布图形是随便画的）：

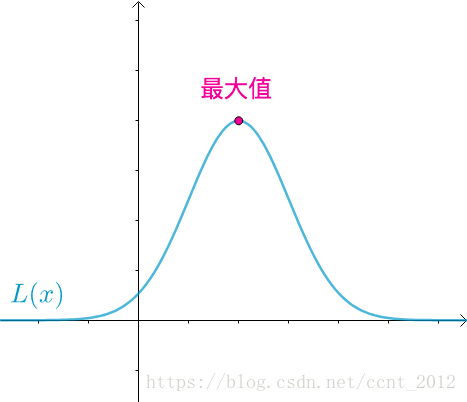
根据极大似然估计的思想，概率最大的最应该出现（既然都出现了，而我又不是“天选之才”，那么自然不会是发生了小概率事件），也就是应该取到下面这点：

当下面这个式子成立时，取得最大值：

$\frac{d}{dx}L(x)=0$

然后高斯想，最小二乘法给出的答案是：

$x=\overline{x}=\frac{x_1+x_2+x_3+x_4+x_5}{5}$

如果最小二乘法是对的，那么 $x=\overline{x}$ 时应该取得最大值，即：

$\frac{d}{dx}L(x)|_{x=\overline{x}}=0$

好，现在可以来解这个微分方程了。最终得到：

$p(\epsilon)={1 \over \sigma\sqrt{2\pi} }\,e^{- {{\epsilon^2 \over 2\sigma^2}}}$

这是什么？这就是正态分布啊。

并且这还是一个充要条件：

$x=\overline{x}\iff p(\epsilon)={1 \over \sigma\sqrt{2\pi} }\,e^{- {{\epsilon^2 \over 2\sigma^2}}}$

也就是说，如果误差的分布是正态分布，那么最小二乘法得到的就是最有可能的值。

那么误差的分布是正态分布吗？

我们相信，误差是由于随机的、无数的、独立的、多个因素造成的，比如之前提到的：

不同厂家的尺子的生产精度不同
尺子材质不同，热胀冷缩不一样
测量的时候心情起伏不定
......

那么根据中心极限定理（参考“为什么正态分布如此常见？”），误差的分布就应该是正态分布。

因为高斯的努力，才真正奠定了最小二乘法的重要地位。

文章最新版本在（有可能会有后续更新）：如何理解最小二乘法？

本文链接：https://blog.csdn.net/ccnt_2012/article/details/81127117

原作者删帖不实内容删帖广告或垃圾文章投诉

智能推荐

python色卡识别_用Python帮小姐姐选口红，人人都是李佳琦-程序员宅基地

文章浏览阅读502次。原标题：用Python帮小姐姐选口红，人人都是李佳琦对于李佳琦，想必知道他的女生要远远多于男生，李佳琦最早由于直播向广大的网友们推荐口红，逐渐走红网络，被大家称作“口红一哥”。不可否认的是，李佳琦的直播能力确实很强，他能够抓住绝大多数人的心理，让大家喜欢看他的直播，看他直播推荐的口红适不适合自己，色号适合什么样子的妆容。为了提升效率，让自己的家人或者女友能够快速的挑选出合适自己妆容的口红色号，今..._获取口红品牌及色号,色值api

linux awk命令NR详解,linux awk命令详解-程序员宅基地

文章浏览阅读3.6k次。简介awk命令的名称是取自三位创始人Alfred Aho 、Peter Weinberger 和 Brian Kernighan姓名的首字母，awk有自己的程序设计语言，设计简短的程序，读入文件，数据排序，处理数据，生成报表等功能。awk 通常用于文本处理和报表生成，最基本功能是在文件或者字符串中基于指定规则浏览和抽取信息，awk抽取信息后，才能进行其他文本操作。awk 通常以文件的一行为处理单位..._linux awk nr

android 网络连接失败!failed to connect to /192.168.1.186(port 8080)_failed to connect to 192.168.88.218:80-程序员宅基地

文章浏览阅读1.3w次，点赞5次，收藏2次。在网上找了一个小时,一直没有头绪,因为上个星期还是好好的,最后看到一个大神的解答,只需要将防火墙关闭就好了.原本向测试功能的,却卡在了登录上.以此记录.另外好像还有种错误是电脑与手机连接的WiFi不同,也可以看看...._failed to connect to 192.168.88.218:80

matlab 多径衰落,利用MATLAB仿真多径衰落信道.doc-程序员宅基地

文章浏览阅读1.9k次。利用MATLAB仿真多种多径衰落信道摘要：移动信道的多径传播引起的瑞利衰落，时延扩展以及伴随接收过程的多普勒频移使接受信号受到严重的衰落，阴影效应会是接受的的信号过弱而造成通信的中断：在信道中存在噪声和干扰，也会是接收信号失真而造成误码，所以通过仿真找到衰落的原因并采取一些信号处理技术来改善信号接收质量显得很重要，这里利用MATLAB对多径衰落信道的波形做一比较。一，多径衰落信道的特点关于多径衰落..._matlab多径衰落工具箱

python对json的操作及实例解析_import json灰色-程序员宅基地

文章浏览阅读1w次，点赞2次，收藏17次。Json简介：Json，全名 JavaScript Object Notation，是一种轻量级的数据交换格式。它基于 ECMAScript (w3c制定的js规范)的一个子集，采用完全独立于编程语言的文本格式来存储和表示数据。简洁和清晰的层次结构使得 JSON 成为理想的数据交换语言。易于人阅读和编写，同时也易于机器解析和生成，并有效地提升网络传输效率。（来自百度百科）python关于json文_import json灰色

mysql实现MHA高可用详细步骤_mysql mha超详细教程-程序员宅基地

文章浏览阅读1.1k次，点赞6次，收藏3次。一、工作原理MHA工作原理总结为以下几条：（1）从宕机崩溃的 master 保存二进制日志事件（binlog events）；（2）识别含有最新更新的 slave ；（3）应用差异的中继日志(relay log) 到其他 slave ；（4）应用从 master 保存的二进制日志事件(binlog events)；（5）通过Manager控制器提升一个 slave 为新 m..._mysql mha超详细教程

随便推点

Linux环境下主从搭建心得（高手勿喷）_linux的java主从策略是什么-程序员宅基地

文章浏览阅读194次。一 java环境安装：1 安装JDK 参考链接地址：https://blog.csdn.net/qq_42815754/article/details/82968464注：有网情况下直接 yum 一键安装：yum -y list java(1)首先执行以下命令查看可安装的jdk版本(2)选择自己需要的jdk版本进行安装，比如这里安装1.8，执行以下命令：yum install -y java-1.8.0-openjdk-devel.x86_64(3)安装完之后，查看安装的jdk 版本，输入以下指令_linux的java主从策略是什么

ACM第四题_acm竞赛题 i 'm from mars-程序员宅基地

文章浏览阅读104次。定义int 类型，由while实现A,B的连续输入，输出A+B的值按Ctrl Z结束循环。#include&lt;iostream&gt;using namespace std;int main(){ int A,B; while(cin&gt;&gt;A&gt;&gt;B) { cout&lt;&lt;A+B&lt;&_acm竞赛题 i 'm from mars

TextView.SetLinkMovementMethod后拦截所有点击事件的原因以及解决方法-程序员宅基地

文章浏览阅读5.2k次。在需要给TextView的某句话添加点击事件的时候，我们一般会使用ClickableSpan来进行富文本编辑。与此同时我们还需要配合 textView.setMovementMethod(LinkMovementMethod.getInstance());方法才能使点击处理生效。但与此同时还会有一个问题：如果我们给父布局添加一个点击事件，需要在点击非链接的时候触发(例如RectclerV..._linkmovementmethod

JAVA实现压缩解压文件_java 解压zip-程序员宅基地

文章浏览阅读1.1w次，点赞6次，收藏31次。JAVA实现压缩解压文件_java 解压zip

JDK8 新特性-Map对key和value分别排序实现_java comparingbykey-程序员宅基地

文章浏览阅读1.3w次，点赞7次，收藏21次。在Java 8 中使用Stream 例子对一个 Map 进行按照keys或者values排序.1. 快速入门在java 8中按照此步骤对map进行排序.将 Map 转换为 Stream 对其进行排序 Collect and return a new LinkedHashMap (保持顺序)Map result = map.entrySet().stream() .sort..._java comparingbykey

GDKOI2021普及Day1总结-程序员宅基地

文章浏览阅读497次。第一次参加GDKOI，考完感觉还可以，结果发现还是不行，有一些地方细节打错，有些失分严重，总结出以下几点：1.大模拟一定要注意，细节打挂就是没分，像T1就是一道大模拟题，马上切了，后面就没想着检查以下，导致有些地方挂掉了，用民间数据一测，才85分。2.十年OI一场空，不开longlonglong longlonglong见祖宗。今天的T2本来想用暴力水点分的，结果没想到longlong→intlong long\to intlonglong→int，40→040\to040→0。3.代码实现能力太差，_gdkoi