深入理解快速傅里叶变换FFT-程序员宅基地
技术标签: FFT FFT理解 快速傅里叶变换 数字信号处理
深入理解快速傅里叶变换FFT
1.FFT介绍
\qquad 离散傅里叶变换(DFT)和卷积是信号处理中两个最基本也是最常用的运算,对于N点序列 x ( n ) x(n) x(n),其DFT变换对定义为:
X ( k ) = ∑ n = 0 N − 1 x ( n ) W N n k k = 0 , 1 , 2 , . . . , N − 1 , W N = e − j 2 π N x ( n ) = 1 N ∑ k = 0 N − 1 X ( k ) W N − n k n = 0 , 1 , . . . , N − 1 \quad\quad\quad \quad X(k)=\sum_{n=0}^{N-1}x(n)W_N^{nk} \quad\quad k=0,1,2,...,N-1,W_N=e^{-j\frac{2\pi}{N}}\\ \quad \\ x(n)=\frac1N\sum_{k=0}^{N-1}X(k)W_N^{-nk} \quad\quad n=0,1,...,N-1 X(k)=n=0∑N−1x(n)WNnkk=0,1,2,...,N−1,WN=e−jN2πx(n)=N1k=0∑N−1X(k)WN−nkn=0,1,...,N−1
首先解释一下,这里的 W N = e − j 2 π N W_N=e^{-j\frac{2\pi}{N}} WN=e−jN2π是一个复数运算,其取得过程如下所示:
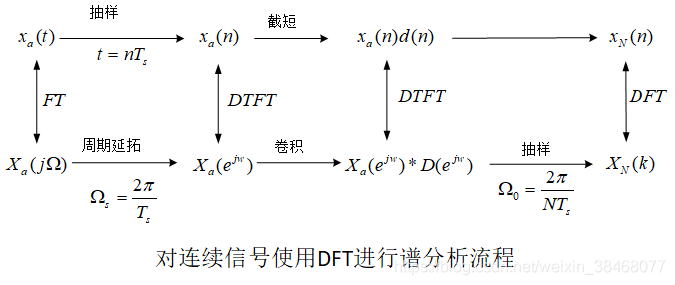
在上图中我们可以知道,这里的 W N W_N WN是经过截短了的。
\qquad 另外在上边的公式中,我们可以看出,由于 W N W_N WN是个复数,又因为k的取值范围在0到N-1,共有N个不同的选择,而对于每一个选定 k k k值的式子,其 n n n的取值范围又从0到N-1,由此可以算出,这 N N N个点 X ( k ) X(k) X(k)需要 N 2 N^2 N2次复数运算和 N ( N − 1 ) N(N-1) N(N−1)次复数加法。再由欧拉公式:
e j w = c o s w + j s i n w e − j w = c o s w − j s i n w e^{jw}=cosw+jsinw\\ \quad \\ e^{-jw}=cosw-jsinw ejw=cosw+jsinwe−jw=cosw−jsinw
将欧拉公式带入 W N W_N WN则有:
W N = e − j π 2 = c o s ( π 2 ) − j s i n ( π 2 ) = − j W_N=e^{-j\frac{\pi}{2}}=cos(\frac{\pi}{2})-jsin(\frac{\pi}{2})=-j WN=e−j2π=cos(2π)−jsin(2π)=−j
由以上公式则也可以分别求得 W N n k W_N^{nk} WNnk,当N等于4时,其表格如下所示:
| W N n k W_N^{nk} WNnk 取N=4 | Value |
|---|---|
| W N 0 W_N^0 WN0 | 1 1 1 |
| W N 1 W_N^1 WN1 | − j -j −j |
| W N 2 W_N^2 WN2 | − 1 -1 −1 |
| W N 3 W_N^3 WN3 | j j j |
| W N 4 W_N^4 WN4 | 1 1 1 |
| W N 6 W_N^6 WN6 | − 1 -1 −1 |
| W N 9 W_N^9 WN9 | − j -j −j |
在上边的运算中我们可以看到,虽然要运行的运算次数有很多,但是结果却是有一定规律的:
W N 0 = W N 4 = 1 W N 1 = W N 9 = − j W N 2 = W N 6 = − 1 W N 3 = j W_N^0=W_N^4=1\\ \quad \\ W_N^1=W_N^9=-j \\ \quad \\ W_N^2=W_N^6=-1\\ \quad \\ W_N^3=j WN0=WN4=1WN1=WN9=−jWN2=WN6=−1WN3=j
\qquad 到了这里,我们或许就看出来了一些规律,此处我们取的N=4,我们发现其结果也是以4为周期的。那么我们现在给出其一般性规律,也就是我们后边的进行快速FFT的基础。
W N 0 = 1 W N N / 2 = − 1 W N N + r = W N r W N ( N / 2 ) + r = − W N r W_N^0=1\\ \quad \\ W_N^{N/2}=-1\\ \quad \\ W_N^{N+r}=W_N^r\\ \quad \\ W_N^{(N/2)+r}=-W_N^r WN0=1WNN/2=−1WNN+r=WNrWN(N/2)+r=−WNr
\qquad 有了上边的规律,我们接下来就以4点DFT来测试一下,根据 X ( k ) X(k) X(k)的计算公式直接计算的话,我们则需要进行 4 2 = 16 4^2=16 42=16次的复数运算,所以我们根据以上得到的规律写成以下矩阵形式:
[ X ( 0 ) X ( 1 ) X ( 2 ) X ( 3 ) ] = [ 1 1 1 1 1 − j − 1 j 1 − 1 1 − 1 1 j − 1 − j ] [ x ( 0 ) x ( 1 ) x ( 2 ) x ( 3 ) ] \left[\begin{matrix} X(0)\\ X(1)\\X(2)\\X(3)\end{matrix}\right]= \left[ \begin{matrix} 1 & 1 & 1 & 1 \\ 1 & -j & -1 & j \\ 1 & -1& 1 & -1 \\ 1 & j & -1 & -j \end{matrix} \right] \left[\begin{matrix} x(0)\\ x(1)\\x(2)\\x(3)\end{matrix}\right] ⎣⎢⎢⎡X(0)X(1)X(2)X(3)⎦⎥⎥⎤=⎣⎢⎢⎡11111−j−1j1−11−11j−1−j⎦⎥⎥⎤⎣⎢⎢⎡x(0)x(1)x(2)x(3)⎦⎥⎥⎤
\qquad 接下来我们就要对上边的矩阵进行一下初等变换,使得其结果仍然等于等式左侧(这里的对右边两个矩阵进行初等变换的目的是为了更加直观的显示出蝶形运算)。
为方便表示,我接下来分别将等式右边的矩阵定义为矩阵A和矩阵B,其形式如下:
A = [ 1 1 1 1 1 − j − 1 j 1 − 1 1 − 1 1 j − 1 − j ] B = [ x ( 0 ) x ( 1 ) x ( 2 ) x ( 3 ) ] A=\left[ \begin{matrix} 1 & 1 & 1 & 1 \\ 1 & -j & -1 & j \\ 1 & -1& 1 & -1 \\ 1 & j & -1 & -j \end{matrix} \right] \qquad\qquad B=\left[\begin{matrix} x(0)\\ x(1)\\x(2)\\x(3)\end{matrix}\right] A=⎣⎢⎢⎡11111−j−1j1−11−11j−1−j⎦⎥⎥⎤B=⎣⎢⎢⎡x(0)x(1)x(2)x(3)⎦⎥⎥⎤
因为矩阵 A B = A E B AB=AEB AB=AEB,则上边的 X ( k ) X(k) X(k)的矩阵即可表示成:
[ X ( 0 ) X ( 1 ) X ( 2 ) X ( 3 ) ] = A [ 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ] B = A [ 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 ] [ 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 ] B = [ 1 1 1 1 1 − 1 − j j 1 1 − 1 − 1 1 − 1 j − j ] [ x ( 0 ) x ( 2 ) x ( 1 ) x ( 3 ) ] \left[\begin{matrix} X(0)\\ X(1)\\X(2)\\X(3)\end{matrix}\right]=A\left[ \begin{matrix} 1 & 0& 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0& 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]B \\ \quad \\\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad =A\left[ \begin{matrix} 1 & 0& 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1& 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]\left[ \begin{matrix} 1 & 0& 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1& 0 & 0 \\ 0 & 0 & 0 & 1 \end{matrix} \right]B \\ \quad \\\quad\quad\quad\quad\quad\quad\quad\quad =\left[ \begin{matrix} 1 & 1 & 1 & 1 \\ 1 & -1 & -j & j \\ 1 & 1& -1 & -1 \\ 1 & -1 & j & -j \end{matrix} \right] \left[\begin{matrix} x(0)\\ x(2)\\x(1)\\x(3)\end{matrix}\right] ⎣⎢⎢⎡X(0)X(1)X(2)X(3)⎦⎥⎥⎤=A⎣⎢⎢⎡1000010000100001⎦⎥⎥⎤B=A⎣⎢⎢⎡1000001001000001⎦⎥⎥⎤⎣⎢⎢⎡1000001001000001⎦⎥⎥⎤B=⎣⎢⎢⎡11111−11−11−j−1j1j−1−j⎦⎥⎥⎤⎣⎢⎢⎡x(0)x(2)x(1)x(3)⎦⎥⎥⎤
\qquad 在上式中,我们对于矩阵A的第二列和第三列互换,将矩阵B的第二行和第三行互换,其结果不变。根据此结果,我们就可以的得出,如下等式:
X ( 0 ) = [ x ( 0 ) + x ( 2 ) ] + [ x ( 1 ) + x ( 3 ) ] X ( 1 ) = [ x ( 0 ) − x ( 2 ) ] − [ x ( 1 ) − x ( 3 ) ] j X ( 2 ) = [ x ( 0 ) + x ( 2 ) ] − [ x ( 1 ) + x ( 3 ) ] X ( 3 ) = [ x ( 0 ) − x ( 2 ) ] + [ x ( 1 ) − x ( 3 ) ] j X(0)=[x(0)+x(2)]+[x(1)+x(3)] \\ \quad \\ X(1)=[x(0)-x(2)]-[x(1)-x(3)]j\\ \quad \\ X(2)=[x(0)+x(2)]-[x(1)+x(3)]\\ \quad \\ X(3)=[x(0)-x(2)]+[x(1)-x(3)]j X(0)=[x(0)+x(2)]+[x(1)+x(3)]X(1)=[x(0)−x(2)]−[x(1)−x(3)]jX(2)=[x(0)+x(2)]−[x(1)+x(3)]X(3)=[x(0)−x(2)]+[x(1)−x(3)]j
\qquad 这样,四点DFT实际上只需要进行一次复数乘法,也就是只需要进行计算 [ x ( 1 ) − x ( 3 ) ] j [x(1)-x(3)]j [x(1)−x(3)]j即可,其实该问题的关键就是如何巧妙的利用W因子的周期性以及对称性,导出一个高效的快速算法。
\qquad 在上边的推导中,我们也可以看到在应用了快速傅里叶变换算法(FFT)后,使得N点的DFT算法的乘法计算量由 N 2 N^2 N2次运算降为 N 2 l o g 2 N \frac{N}{2}log_2N 2Nlog2N次,大大加快了计算速度。
2.时间抽取(DIT)基2 FFT算法
在介绍这个之前,我先介绍一下FFT的核心思想:

对于N点的DFT算法,我们习惯上使用 N = 2 M N=2^M N=2M来进行计算,根据DFT正变换的公式:
X ( k ) = ∑ n = 0 N − 1 x ( n ) W N n k k = 0 , 1 , 2 , . . . , N − 1 , W N = e − j 2 π N X(k)=\sum_{n=0}^{N-1}x(n)W_N^{nk} \quad\quad k=0,1,2,...,N-1,W_N=e^{-j\frac{2\pi}{N}} X(k)=n=0∑N−1x(n)WNnkk=0,1,2,...,N−1,WN=e−jN2π
中我们将 x ( n ) x(n) x(n)分为奇、偶两部分,也就是令 n = 2 r 、 n = 2 r + 1 r = 0.1 , . . . , N 2 − 1 n=2r 、n=2r+1 \qquad r=0.1,..., \frac{N}{2}-1 n=2r、n=2r+1r=0.1,...,2N−1于是上式也就可以改写为:
X ( k ) = ∑ r = 0 N / 2 − 1 x ( 2 r ) W N 2 r k + ∑ r = 0 N / 2 − 1 x ( 2 r + 1 ) W N ( 2 r + 1 ) k = ∑ r = 0 N / 2 − 1 x ( 2 r ) W N / 2 2 r k + ∑ r = 0 N / 2 − 1 x ( 2 r + 1 ) W N / 2 ( 2 r + 1 ) k X(k)=\sum_{r=0}^{N/2-1}x(2r)W_N^{2rk}+ \sum_{r=0}^{N/2-1}x(2r+1)W_N^{(2r+1)k}\\ \quad \\\quad\quad\quad =\sum_{r=0}^{N/2-1}x(2r)W_{N/2}^{2rk}+ \sum_{r=0}^{N/2-1}x(2r+1)W_{N/2}^{(2r+1)k} X(k)=r=0∑N/2−1x(2r)WN2rk+r=0∑N/2−1x(2r+1)WN(2r+1)k=r=0∑N/2−1x(2r)WN/22rk+r=0∑N/2−1x(2r+1)WN/2(2r+1)k
式中 W N / 2 = e − j 2 π N / 2 = e − j π W_{N/2}=e^{-j\frac{2\pi}{N/2}}=e^{-j\pi} WN/2=e−jN/22π=e−jπ
现在令 A ( k ) 、 B ( k ) A(k)、B(k) A(k)、B(k):分别代表 X ( k ) X(k) X(k)的偶数项和奇数项:
A ( k ) = ∑ r = 0 N / 2 − 1 x ( 2 r ) W N / 2 2 r k k = 0 , 1 , . . . , N 2 − 1 B ( k ) = ∑ r = 0 N / 2 − 1 x ( 2 r + 1 ) W N / 2 ( 2 r + 1 ) k k = 0 , 1 , . . . , N 2 − 1 A(k)=\sum_{r=0}^{N/2-1}x(2r)W_{N/2}^{2rk} \qquad k=0,1,...,\frac N2-1 \\ \quad \\\quad\quad\quad B(k)=\sum_{r=0}^{N/2-1}x(2r+1)W_{N/2}^{(2r+1)k}\qquad k=0,1,...,\frac N2-1 \\ \quad \\ A(k)=r=0∑N/2−1x(2r)WN/22rkk=0,1,...,2N−1B(k)=r=0∑N/2−1x(2r+1)WN/2(2r+1)kk=0,1,...,2N−1
那么, X ( k ) X(k) X(k)则可以表示为:
X ( k ) = A ( k ) + W N k B ( k ) , k = 0 , 1 , . . . , N 2 − 1 X(k)=A(k)+W_N^kB(k),\qquad k=0,1,...,\frac N2-1 X(k)=A(k)+WNkB(k),k=0,1,...,2N−1
\qquad 但是此时我们仅可以根据该式子,算出来一半的 X ( k ) X(k) X(k),也就是 X ( 0 ) 、 X ( 1 ) X(0)、X(1) X(0)、X(1),而其余两项该式是无法求出的。具体的想要求出其余两项则需要公式:
X ( k + N 2 ) = A ( k + N 2 ) + W N k + N 2 B ( k + N 2 ) = A ( k + N 2 ) − W N k B ( k + N 2 ) = A ( k ) − W N k B ( k ) , k = 0 , 1 , . . . , N 2 − 1 X(k+\frac N2)=A(k+\frac N2)+W_N^{k+\frac N2}B(k+\frac N2)\\ \quad \\\quad\quad\quad\quad =A(k+\frac N2)-W_N^{k}B(k+\frac N2)\\ \quad \\\quad\quad\quad\quad\quad\quad\quad\quad = A(k)-W_N^{k}B(k)\quad ,k=0,1,...,\frac N2-1 X(k+2N)=A(k+2N)+WNk+2NB(k+2N)=A(k+2N)−WNkB(k+2N)=A(k)−WNkB(k),k=0,1,...,2N−1
\qquad 此处的 A ( k + N 2 ) A(k+\frac N2) A(k+2N)可以理解为偶数项的下一个周期,所以此处可以直接看为 A ( k ) A(k) A(k)。
所以用 A ( k ) 、 B ( k ) A(k)、B(k) A(k)、B(k)可以完整的表示 X ( k ) X(k) X(k),当N=4时, A ( k ) 、 B ( k ) A(k)、B(k) A(k)、B(k)以及 X ( k ) X(k) X(k)的关系如下所示:
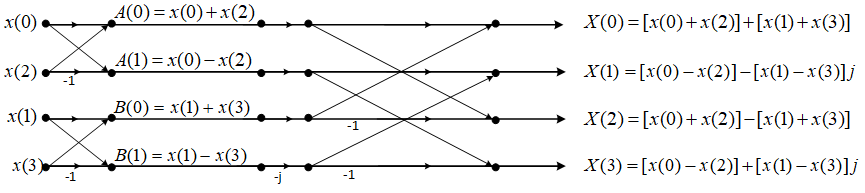
\qquad 这里我只展示了当N=4的时候,当N=8的时候,则我们需要继续将 A ( k ) A(k) A(k)分为偶数项 C ( k ) C(k) C(k)与奇数项 D ( k ) D(k) D(k)之和,将 B ( k ) B(k) B(k)分为偶数项 E ( k ) E(k) E(k)与奇数项 F ( k ) F(k) F(k)之和,其 k k k值取值范围为 k = 0 , 1 , . . . , N 4 − 1 k=0,1,...,\frac N4-1 k=0,1,...,4N−1。
\qquad 若N=16,或者更高的幂,可以按照这样的方法继续分下去,直到分到两点的DFT为止。
介绍到这里,相信大家都已经很明白了,该算法是将时间 n n n按照奇、偶分开,所以被称为时间抽取算法。
3.FFT算法的一般规律
\qquad 我们知道,对于进行FFT快速傅里叶变换,找到W因子的周期性以及对称性是非常关键的。比如当N=4的时候, x ( 0 ) 、 x ( 1 ) 、 x ( 2 ) 、 x ( 3 ) x(0)、x(1)、x(2)、x(3) x(0)、x(1)、x(2)、x(3)的排列顺序为 x ( 0 ) 、 x ( 2 ) 、 x ( 1 ) 、 x ( 3 ) x(0)、x(2)、x(1)、x(3) x(0)、x(2)、x(1)、x(3)。如果这个顺序让我们自己取记忆的话,如果当N值小的时候或许还可以记住,但是如果当N大的时候,这样单纯记忆就显得不切实际。为此,我们能否找到它的排列规律显得尤为重要,以下我将分别以N=4和N=8来介绍这一方法:
当N=4时其表格如下:
| n n n | x ( n ) x(n) x(n) | X ( k ) X(k) X(k) | k k k |
|---|---|---|---|
| 0 | 00 | 000 | 0 |
| 2 | 10 | 001 | 1 |
| 1 | 01 | 010 | 2 |
| 3 | 11 | 011 | 3 |
当N=8时其表格如下:
| n n n | x ( n ) x(n) x(n) | X ( k ) X(k) X(k) | k k k |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 4 | 100 | 001 | 1 |
| 2 | 010 | 010 | 2 |
| 6 | 110 | 011 | 3 |
| 1 | 001 | 100 | 4 |
| 5 | 101 | 101 | 5 |
| 3 | 011 | 110 | 6 |
| 7 | 111 | 111 | 7 |
仔细观看的话,我们或许会发现 x ( n ) x(n) x(n)的取值顺序也是按照二进制加法,但是这个加法是在左侧加,而 X ( k ) X(k) X(k)则是在右侧加。也就是说是 X ( k ) X(k) X(k)的对称。有了这个规律,那么不管 N = 2 M N=2^M N=2M的值取多大,我们都可以快速的排列出其顺序,这对于加快运算速度是有很大帮助的。
因为 M = l o g 2 N M=log_2N M=log2N所以将N点DFT可以分成M级,当N等于8时,M=3,从左到右可以分为 m = 0 , m = 1 , m = 2 m=0,m=1,m=2 m=0,m=1,m=2三级。接下来我将展示8点DFT时间抽取算法的信号流图:
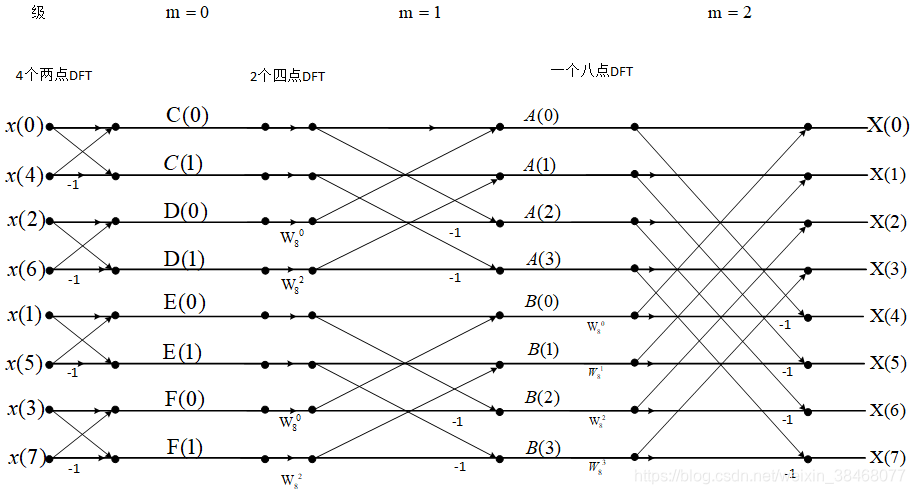
这里我们或许就会看到如下现象:
在每一个向上连接的线的下边都要乘一个 W r W^r Wr因子,
每一个向下连接的线的搭档都需要乘-1。
下面我将会来介绍一下 W r W^r Wr因子的分布情况:
| m m m 值(第几级) | 对应的 W r W^r Wr因子分布 |
|---|---|
| m = 0 m=0 m=0 级 | W 2 r , r = 0 W_2^r,r=0 W2r,r=0 |
| m = 1 m=1 m=1 级 | W 4 r , r = 0 , 1 W_4^r,r=0,1 W4r,r=0,1 |
| m = 2 m=2 m=2 级 | W 8 r , r = 0 , 1 , 2 , 3 W_8^r,r=0,1,2,3 W8r,r=0,1,2,3 |
| … | … |
| m = M − 1 m=M-1 m=M−1 级 | W N r , r = 0 , 1 , . . . , N 2 − 1 W_N^r,r=0,1,...,\frac N2-1 WNr,r=0,1,...,2N−1 |
如果你仔细看我的流图的话或许会发现,我在m=1的时候,使用了因子 W 8 0 , W 8 2 W_8^0,W_8^2 W80,W82,在这里我使用这个因子只是为了方便和后边的比较,其实这个还是有一个代换公式的:
W 8 0 = W 4 0 , W 8 2 = W 4 1 W_8^0=W_4^0,W_8^2=W_4^1 W80=W40,W82=W41
4.后续
该部分留作后边对于FFT的更加深入的理解。
智能推荐
c# 调用c++ lib静态库_c#调用lib-程序员宅基地
文章浏览阅读2w次,点赞7次,收藏51次。四个步骤1.创建C++ Win32项目动态库dll 2.在Win32项目动态库中添加 外部依赖项 lib头文件和lib库3.导出C接口4.c#调用c++动态库开始你的表演...①创建一个空白的解决方案,在解决方案中添加 Visual C++ , Win32 项目空白解决方案的创建:添加Visual C++ , Win32 项目这......_c#调用lib
deepin/ubuntu安装苹方字体-程序员宅基地
文章浏览阅读4.6k次。苹方字体是苹果系统上的黑体,挺好看的。注重颜值的网站都会使用,例如知乎:font-family: -apple-system, BlinkMacSystemFont, Helvetica Neue, PingFang SC, Microsoft YaHei, Source Han Sans SC, Noto Sans CJK SC, W..._ubuntu pingfang
html表单常见操作汇总_html表单的处理程序有那些-程序员宅基地
文章浏览阅读159次。表单表单概述表单标签表单域按钮控件demo表单标签表单标签基本语法结构<form action="处理数据程序的url地址“ method=”get|post“ name="表单名称”></form><!--action,当提交表单时,向何处发送表单中的数据,地址可以是相对地址也可以是绝对地址--><!--method将表单中的数据传送给服务器处理,get方式直接显示在url地址中,数据可以被缓存,且长度有限制;而post方式数据隐藏传输,_html表单的处理程序有那些
PHP设置谷歌验证器(Google Authenticator)实现操作二步验证_php otp 验证器-程序员宅基地
文章浏览阅读1.2k次。使用说明:开启Google的登陆二步验证(即Google Authenticator服务)后用户登陆时需要输入额外由手机客户端生成的一次性密码。实现Google Authenticator功能需要服务器端和客户端的支持。服务器端负责密钥的生成、验证一次性密码是否正确。客户端记录密钥后生成一次性密码。下载谷歌验证类库文件放到项目合适位置(我这边放在项目Vender下面)https://github.com/PHPGangsta/GoogleAuthenticatorPHP代码示例://引入谷_php otp 验证器
【Python】matplotlib.plot画图横坐标混乱及间隔处理_matplotlib更改横轴间距-程序员宅基地
文章浏览阅读4.3k次,点赞5次,收藏11次。matplotlib.plot画图横坐标混乱及间隔处理_matplotlib更改横轴间距
docker — 容器存储_docker 保存容器-程序员宅基地
文章浏览阅读2.2k次。①Storage driver 处理各镜像层及容器层的处理细节,实现了多层数据的堆叠,为用户 提供了多层数据合并后的统一视图②所有 Storage driver 都使用可堆叠图像层和写时复制(CoW)策略③docker info 命令可查看当系统上的 storage driver主要用于测试目的,不建议用于生成环境。_docker 保存容器
随便推点
网络拓扑结构_网络拓扑csdn-程序员宅基地
文章浏览阅读834次,点赞27次,收藏13次。网络拓扑结构是指计算机网络中各组件(如计算机、服务器、打印机、路由器、交换机等设备)及其连接线路在物理布局或逻辑构型上的排列形式。这种布局不仅描述了设备间的实际物理连接方式,也决定了数据在网络中流动的路径和方式。不同的网络拓扑结构影响着网络的性能、可靠性、可扩展性及管理维护的难易程度。_网络拓扑csdn
JS重写Date函数,兼容IOS系统_date.prototype 将所有 ios-程序员宅基地
文章浏览阅读1.8k次,点赞5次,收藏8次。IOS系统Date的坑要创建一个指定时间的new Date对象时,通常的做法是:new Date("2020-09-21 11:11:00")这行代码在 PC 端和安卓端都是正常的,而在 iOS 端则会提示 Invalid Date 无效日期。在IOS年月日中间的横岗许换成斜杠,也就是new Date("2020/09/21 11:11:00")通常为了兼容IOS的这个坑,需要做一些额外的特殊处理,笔者在开发的时候经常会忘了兼容IOS系统。所以就想试着重写Date函数,一劳永逸,避免每次ne_date.prototype 将所有 ios
如何将EXCEL表导入plsql数据库中-程序员宅基地
文章浏览阅读5.3k次。方法一:用PLSQL Developer工具。 1 在PLSQL Developer的sql window里输入select * from test for update; 2 按F8执行 3 打开锁, 再按一下加号. 鼠标点到第一列的列头,使全列成选中状态,然后粘贴,最后commit提交即可。(前提..._excel导入pl/sql
Git常用命令速查手册-程序员宅基地
文章浏览阅读83次。Git常用命令速查手册1、初始化仓库git init2、将文件添加到仓库git add 文件名 # 将工作区的某个文件添加到暂存区 git add -u # 添加所有被tracked文件中被修改或删除的文件信息到暂存区,不处理untracked的文件git add -A # 添加所有被tracked文件中被修改或删除的文件信息到暂存区,包括untracked的文件...
分享119个ASP.NET源码总有一个是你想要的_千博二手车源码v2023 build 1120-程序员宅基地
文章浏览阅读202次。分享119个ASP.NET源码总有一个是你想要的_千博二手车源码v2023 build 1120
【C++缺省函数】 空类默认产生的6个类成员函数_空类默认产生哪些类成员函数-程序员宅基地
文章浏览阅读1.8k次。版权声明:转载请注明出处 http://blog.csdn.net/irean_lau。目录(?)[+]1、缺省构造函数。2、缺省拷贝构造函数。3、 缺省析构函数。4、缺省赋值运算符。5、缺省取址运算符。6、 缺省取址运算符 const。[cpp] view plain copy_空类默认产生哪些类成员函数