图像频率域分析之傅里叶变换_研究傅里叶时域图像时频率是不变的吗-程序员宅基地
技术标签: 计算机视觉 图像处理 Computer Vision
Overview
欢迎访问 持续更新:https://cgabc.xyz/posts/bcb5a7d3/
傅里叶变换基础
傅里叶级数
法国数学家傅里叶发现,任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示(选择正弦函数与余弦函数作为基函数是因为它们是正交的),即 任何周期信号都可以表示成一系列正弦信号的叠加
- 三角形式
f ( t ) = a 0 2 + ∑ k = 1 + ∞ [ a k c o s ( n ω t ) + b k s i n ( n ω t ) ] , a 0 2 = 1 T ∫ − T 2 T 2 f ( t ) d t f(t) = \frac{a_0}{2} + \sum_{k=1}^{+\infty} \big[ a_k cos (n \omega t) + b_k sin (n \omega t) \big], \quad \frac{a_0}{2} = \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) dt f(t)=2a0+k=1∑+∞[akcos(nωt)+bksin(nωt)],2a0=T1∫−2T2Tf(t)dt
- 复指数形式
f ( t ) = 1 T ∑ n = − ∞ + ∞ [ ∫ − T 2 T 2 f ( τ ) e − j ω n τ d τ ] e j ω n t f(t) = \frac{1}{T} \sum_{n=-\infty}^{+\infty} [ \int_{-\frac{T}{2}}^{\frac{T}{2}} f(\tau)e^{-j\omega_n\tau} d\tau ] e^{j\omega_nt} f(t)=T1n=−∞∑+∞[∫−2T2Tf(τ)e−jωnτdτ]ejωnt
基波角频率 ω = 2 π T \omega = \frac{2\pi}{T} ω=T2π , T T T 为 f ( t ) f(t) f(t) 的周期, j j j 为虚数单位
傅里叶积分
复指数形式
f ( t ) = 1 2 π ∫ − ∞ + ∞ [ ∫ − ∞ + ∞ f ( τ ) e − j ω τ d τ ] e j ω t d ω f(t) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} [ \int_{-\infty}^{+\infty} f(\tau)e^{-j\omega\tau} d\tau ] e^{j\omega t} d\omega f(t)=2π1∫−∞+∞[∫−∞+∞f(τ)e−jωτdτ]ejωtdω
傅里叶变换
一维连续傅里叶变换
正变换 为
F ( ω ) = ∫ − ∞ + ∞ f ( t ) e − j ω t d t F(\omega) = \int_{-\infty}^{+\infty} f(t) e^{-j\omega t} dt F(ω)=∫−∞+∞f(t)e−jωtdt
逆变换 为
f ( t ) = 1 2 π ∫ − ∞ + ∞ F ( ω ) e j ω t d ω f(t) = \frac{1}{2\pi} \int_{-\infty}^{+\infty} F(\omega) e^{j\omega t} d\omega f(t)=2π1∫−∞+∞F(ω)ejωtdω
一维离散傅里叶变换
正变换 为
F ( u ) = ∑ x = 0 M − 1 f ( x ) e − j 2 π u x M F(u) = \sum_{x=0}^{M-1} f(x) e^{-j2\pi \frac{ux}{M}} F(u)=x=0∑M−1f(x)e−j2πMux
则
F ( 0 ) = ∑ x = 0 M − 1 f ( x ) F(0) = \sum_{x=0}^{M-1} f(x) F(0)=x=0∑M−1f(x)
反变换 为
f ( x ) = 1 M ∑ u = 0 M − 1 F ( u ) e j 2 π u x M f(x) = \frac{1}{M} \sum_{u=0}^{M-1} F(u) e^{j2\pi \frac{ux}{M}} f(x)=M1u=0∑M−1F(u)ej2πMux
对于反变换式前的系数 1 M \frac{1}{M} M1 ,也可放在正变换中,只要保证正变换与反变换之前的系数乘积为 1 M \frac{1}{M} M1 即可。
二维离散傅里叶变换
正变换
二维离散傅里叶变换:
F [ f ( x , y ) ] = F ( u , v ) = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) e − j 2 π ( u x M + v y N ) F[f(x,y)] = F(u,v) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x,y) e^{-j2\pi(\frac{ux}{M}+\frac{vy}{N})} F[f(x,y)]=F(u,v)=x=0∑M−1y=0∑N−1f(x,y)e−j2π(Mux+Nvy)
当 ( u , v ) (u,v) (u,v) 等于 ( 0 , 0 ) (0,0) (0,0) 时,直流分量 为:
F ( 0 , 0 ) = ∑ x = 0 M − 1 ∑ y = 0 N − 1 f ( x , y ) F(0,0) = \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x,y) F(0,0)=x=0∑M−1y=0∑N−1f(x,y)
幅度谱 为:
A ( u , v ) = ∣ F ( u , v ) ∣ = R e a l ( u , v ) 2 + I m a g e ( u , u ) 2 A(u,v) = |F(u,v)| = \sqrt{Real(u,v)^2 + Image(u,u)^2} A(u,v)=∣F(u,v)∣=Real(u,v)2+Image(u,u)2
功率谱 为:
P ( u , v ) = ∣ F ( u , v ) ∣ 2 = R e a l ( u , v ) 2 + I m a g e ( u , u ) 2 P(u,v) = |F(u,v)|^{2} = Real(u,v)^2 + Image(u,u)^2 P(u,v)=∣F(u,v)∣2=Real(u,v)2+Image(u,u)2
相位谱 为:
ϕ ( u , v ) = a r c t a n I m a g e ( u , v ) R e a l ( u , v ) \phi(u,v) = arctan \frac{Image(u,v)}{Real(u,v)} ϕ(u,v)=arctanReal(u,v)Image(u,v)
通过 幅度谱 和 相位谱,我们也能合成 其傅里叶变换(频谱):
F ( u , v ) = A ( u , v ) e j ϕ ( u , v ) = A ( c o s ϕ + j s i n ϕ ) (省略(u,v),应用 欧拉公式) = A c o s ϕ + j A s i n ϕ \begin{aligned} F(u,v) &= A(u,v)e^{j\phi(u,v)} \\ &= A( cos \phi + jsin \phi ) \quad \text{(省略(u,v),应用 欧拉公式)}\\ &= Acos\phi + jAsin\phi \end{aligned} F(u,v)=A(u,v)ejϕ(u,v)=A(cosϕ+jsinϕ)(省略(u,v),应用 欧拉公式)=Acosϕ+jAsinϕ
注意:
- 上面式子中的 j j j 为 虚数单位
- R e a l ( u , v ) Real(u,v) Real(u,v) 为 复数的 实部
- I m a g e ( u , v ) Image(u,v) Image(u,v) 为 复数的 虚部
反变换
f ( x , y ) = F − 1 ( u , v ) = 1 M N ∑ u = 0 M − 1 ∑ v = 0 N − 1 F ( u , v ) e j 2 π ( u x M + v y N ) f(x,y) = F^{-1}(u,v) = \frac{1}{MN} \sum_{u=0}^{M-1} \sum_{v=0}^{N-1} F(u,v) e^{j2\pi(\frac{ux}{M}+\frac{vy}{N})} f(x,y)=F−1(u,v)=MN1u=0∑M−1v=0∑N−1F(u,v)ej2π(Mux+Nvy)
卷积
∫ − ∞ + ∞ f 1 ( τ ) f 2 ( t − τ ) d τ = f 1 ( t ) ∗ f 2 ( t ) \int_{-\infty}^{+\infty} f_1(\tau)f_2(t-\tau) d\tau = f_1(t) * f_2(t) ∫−∞+∞f1(τ)f2(t−τ)dτ=f1(t)∗f2(t)
卷积定理
函数卷积的傅立叶变换是函数傅立叶变换的乘积
- 时域卷积定理:时域内的卷积对应频域内的乘积
F [ f 1 ( t ) ∗ f 2 ( t ) ] = F 1 ( ω ) ⋅ F 2 ( ω ) F[f_1(t) * f_2(t)] = F_1(\omega) \cdot F_2(\omega) F[f1(t)∗f2(t)]=F1(ω)⋅F2(ω)
- 频域卷积定理:频域内的卷积对应时域内的乘积
F [ f 1 ( t ) ⋅ f 2 ( t ) ] = 1 2 π F 1 ( ω ) ∗ F 2 ( ω ) F[f_1(t) \cdot f_2(t)] = \frac{1}{2\pi} F_1(\omega) * F_2(\omega) F[f1(t)⋅f2(t)]=2π1F1(ω)∗F2(ω)
数字图像DFT
借用知乎大神Heinrich的一张图,来个感性认识:
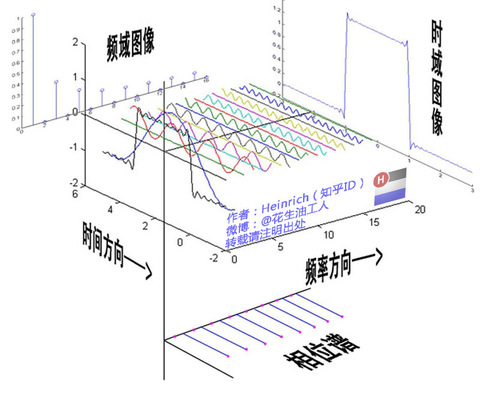
空间域和频域
- 空间域:在图像处理中,时域可以理解为 空间域 或者 图像空间,处理对象为图像像元;
- 频域:以 空间频率 为自变量描述图像的特征,可以将一幅图像像元值在空间上的变化分解为具有不同振幅、空间频率和相位的简振函数的线性叠加,图像中各种空间频率成分的组成和分布称为 图像频谱
空间域与频域可互相转换,对图像施行 二维离散傅立叶变换 或 小波变换 ,可以将图像由空间域转换到频域;通过 对应的反变换 又可转换回空间域图像,即人可以直接识别的图像。
图像频域滤波
二维数字图像的滤波主要分为 空间域滤波 和 频域滤波:
-
空间域滤波: 用各种模板直接与图像进行 卷积运算,实现对图像的处理,这种方法直接对图像空间操作,操作简单
-
频域滤波: 在实现某些图像处理的时候,频域的处理比空间域更简单;对于在空间域上的数字图像,根据 卷积定理 可以通过 傅立叶变换 将 空域卷积滤波 变换为 频域滤波,然后再将频域滤波处理后的图像 反变换 回空间域
基本步骤
图像频域滤波步骤为(频谱图中心化):
- 计算 原始图像 f ( x , y ) f(x,y) f(x,y) 的DFT,得到 频谱 F ( u , v ) F(u,v) F(u,v)
- 中心化:将频谱 F ( u , v ) F(u,v) F(u,v) 的零频点移动到频谱图的中心位置
- 计算 滤波器函数 H ( u , v ) H(u,v) H(u,v) 与 F ( u , v ) F(u,v) F(u,v) 的乘积 G ( u , v ) = F ( u , v ) ⋅ H ( u , v ) G(u,v) = F(u,v) \cdot H(u,v) G(u,v)=F(u,v)⋅H(u,v)
- 反中心化:将频谱 G ( u , v ) G(u,v) G(u,v) 的零频点移回到频谱图的左上角位置
- 计算上一步计算结果的 傅里叶反变换 g ( x , y ) g(x,y) g(x,y)
- 取 g ( x , y ) g(x,y) g(x,y) 的 实部 作为最终滤波后的结果图像
上面步骤是对 图像频谱 进行 中心变换;我们也可以先对 原始图像 进行 中心变换,再计算其 频谱图,滤波步骤如下(原始图中心化):
- 原始图像 f ( x , y ) f(x,y) f(x,y) 中心变换: f ( x , y ) ⋅ ( − 1 ) ( x + y ) f(x,y) \cdot (-1)^{(x+y)} f(x,y)⋅(−1)(x+y)
- 计算上一步计算结果的DFT,得到其 频谱 F ( u , v ) F(u,v) F(u,v)
- 计算 滤波器函数 H ( u , v ) H(u,v) H(u,v) 与 F ( u , v ) F(u,v) F(u,v) 的乘积 G ( u , v ) = F ( u , v ) ⋅ H ( u , v ) G(u,v) = F(u,v) \cdot H(u,v) G(u,v)=F(u,v)⋅H(u,v)
- 计算 G ( u , v ) G(u,v) G(u,v) 的 傅里叶反变换 g ( x , y ) g(x,y) g(x,y)
- 取 g ( x , y ) g(x,y) g(x,y) 的 实部
- 上一步计算结果 乘以 ( − 1 ) ( x + y ) (-1)^{(x+y)} (−1)(x+y) 作为最终滤波后的结果图像
滤波能否取得理想结果的关键取决于上面的 滤波器函数 H ( u , v ) H(u,v) H(u,v) 。
这时让我想到了《自动控制理论》中的 传递函数 G ( s ) G(s) G(s),定义为:初始条件为零的线性定常系统输出的拉普拉斯变换与输入的拉普拉斯变换之比。
下面以 控制论的思想 给出图像频域滤波的示意框图:
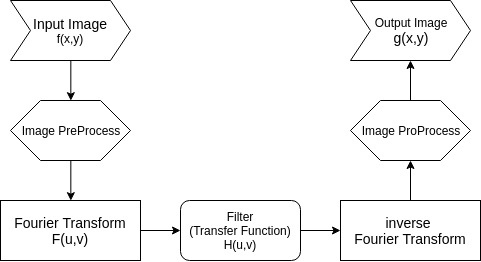
图像频率特性分析
频谱图上的每一个像素点都代表一个频率值,幅值由像素点亮度变码而得。对于一幅图像,图像信号的 频率特性 如下:
- 直流分量 表示预想的平均灰度
- 低频分量 代表了大面积背景区域和缓慢变化部分
- 高频分量 代表了它的边缘、细节、跳跃部分以及颗粒噪声
- 振幅 描述了图像灰度的亮度
- 相位 决定了图像是什么样子
数字图像的二维离散傅立叶变换所得的结果的频域成分如下图所示,左上角是直流成分,变换结果四个角周围对应于低频成分,中央部分对应于高频部分
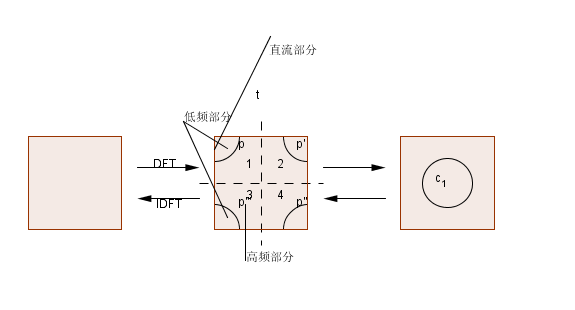
为了便于观察,常常采取 换位 方法使直流成分出现在窗口的中央(中心化),变换后中心为低频,向外是高频。
在频域,可以很方便的实现 图像的锐化和模糊:
- 截取频率的低频分量,对其作傅立叶反变换,得到的就是模糊后的图像,即 低通滤波
- 截取频率的高频分量,对其作傅立叶反变换,得到的就是锐化后的图像,即 高通滤波
图像滤波实践
下面,我们以 lena.bmp(点此下载) 图像进行滤波实践。
Python分析
(1)加载图像,并转换为 灰度图 为
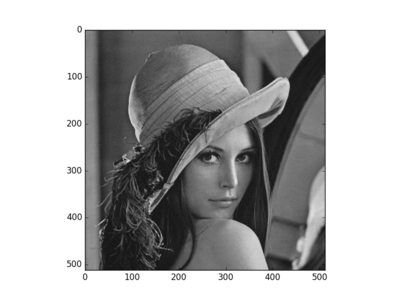
(2)对其 快速傅里叶变换,并经过 中心变换,得到 频率谱 和 相位谱

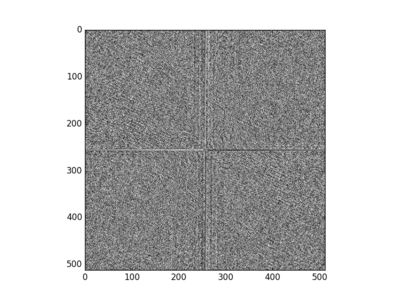
(3)分别截取 频谱图 的 低频部分(中间部分) 和 高频分量(四周部分)
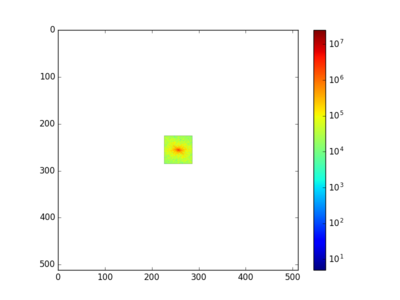

(4)对以上处理过的频谱图分别进行 反中心化、傅里叶反变换、取实部,得到 低通滤波 和 高通滤波 后的图像

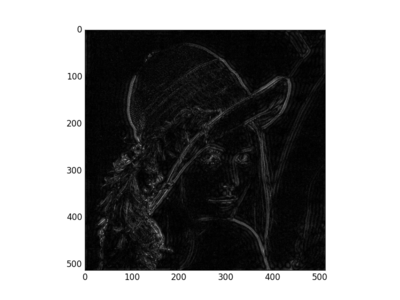
C++分析
使用 CImg 和 FFTW库 对 lena图像进行傅里叶变换(源代码见文末),结果如下

源代码
以上所有代码均存储在我的Github仓库:
- Python Code: cggos/cgocv_app/cv_py
- C++ Code: cggos/cgocv_app/image_process/fftw_demos
参考资料
智能推荐
Subnet简介-程序员宅基地
文章浏览阅读2.9w次,点赞2次,收藏13次。Subnet(子网)在一般的概念中,有两个基本含义:1 这个子网的网段(CIDR)和IP版本;2 这个子网的路由(含默认路由)。事实上,Subnet模型也确实有这两个字段cidr和ip_version,分别表示一个子网的网段和IP版本。另外Subnet模型还有两字段gateway_ip和host_routes,表示一个子网的路由信息。gateway_ip是这个子网的默认网关IP。host_rout..._subnet
HBase的列族必须提前定义-程序员宅基地
文章浏览阅读282次,点赞4次,收藏7次。在HBase中,列族(Column Family)必须在创建表时提前定义,而列(Column)是动态添加的,无需提前定义。一旦表创建完成并列族定义好之后,可以动态地向表中的列族中添加新的列,而无需修改表的结构。2. **列是动态添加的:** 列是在列族内动态添加的,无需提前定义。而列是动态添加的,可以根据需要随时向列族中添加新的列。1. **列族必须提前定义:** 在创建HBase表时,需要指定表的列族,每个列族都需要提前定义。列族的定义是静态的,一旦表创建完成并列族定义好之后,列族的结构就不能再改变了。
人工智能伦理框架:如何建立AI技术的道德规范-程序员宅基地
文章浏览阅读365次,点赞6次,收藏9次。1.背景介绍人工智能(AI)技术的发展已经进入了关键时期,它正在改变我们的生活、经济和社会结构。然而,随着AI技术的不断发展,也引发了一系列道德、伦理和法律问题。为了确保AI技术的可持续发展和社会接受,我们需要建立一个人工智能伦理框架,以指导AI技术的研发和应用。在过去的几年里,许多学者、企业家、政府机构和非政府组织都开始关注AI伦理问题,并提出了许多关于AI伦理的建议和规范。然而,这些建..._人工智能道德框架
我个人总结的Halcon内存管理心得笔记,关于C#/C++内存释放_halcon dispose-程序员宅基地
文章浏览阅读1.4w次,点赞15次,收藏105次。Halcon容易造成内存增长或泄露。怎么办?C#1、变量用完之后,Dispose()和置Null。在Halcon18以上版本,Halcon已经提供了Dispose()方法进行释放,那么在低版本中HTuple类型占用的内存怎么释放呢?其实,Halcon中提供一个叫UnPinTuple()的方法,该方法就是官方用来进行释放HTuple的!所以,使用后的变量如不再继续使用的可以用该方法进行清除释放。2、图像尽量不要复制,固定在一个变量进行处理。3、在软件内存占用率高,并且软件闲置的时候,._halcon dispose
SQL 语言及查询优化技巧-程序员宅基地
文章浏览阅读719次。SQL (Structured Query Language,结构化查询语言),一种专门用来管理关系数据库(RDBMS)的语言。它用于存取、操纵和维护关系数据库中的数据,尤其是保存着各种相关信息的表格。由于其标准化,可移植性强,而且易于学习和应用,所以在各个行业都得到广泛应用。与其他编程语言相比,SQL 的学习难度较低,语法简单,执行效率高。同时,SQL 有完善的函数库支持,能够实现丰富的数据处理功能,如数据检索、过滤、排序、汇总等。
java程序:调用百度api进行情感分析-程序员宅基地
文章浏览阅读684次,点赞2次,收藏4次。源码:package com.jeson.ceshi;import java.util.HashMap;import org.json.JSONObject;import com.baidu.aip.nlp.AipNlp;public class demo { //设置APPID/AK/SK public static final ..._java百度云情感api
随便推点
linux操作系统有哪些_linux系统有什么-程序员宅基地
文章浏览阅读7.4k次。微信设置水滴昵称,个性中带点萌区别:(1)Linux速度比较快,安全性比windows好 (2)有很多软件只能在windows里运行 ,与Linux兼容的软件正在开发中. (3)Linux适用在网络方面. (4)Linux的操作比较复杂,windows的比较简单. Linux和Windows的区别 和Linux 一样,Windows系列是完全的多任务操作系统。它们支持同样的用户接口 、网络和安全性。但是,Linux和Windows的真正区别在于,Linux 事实上是Unix 的一种版本,而且来_linux系统有什么
K8s 为什么要弃用 Docker_kubenetes为什么1.24弃用docker-程序员宅基地
文章浏览阅读1w次,点赞15次,收藏24次。最近在学习容器技术的过程中,看到有关于Kubernetes“弃用 Docker”的事情,担心现在学 Docker 是否还有价值,是否现在就应该切换到 containerd 或者是其他 runtime。随着深入了解,这些疑虑的确是有些道理。三年前,Kubernetes 放出消息要“弃用 Docker”的时候,确确实实在 Kubernetes 社区里掀起了一场“轩然大波”,影响甚至波及到社区之外,也导致 Kubernetes 不得不写了好几篇博客来反复解释这么做的原因。_kubenetes为什么1.24弃用docker
IDEA 简单自动化部署 Alibaba Cloud Toolkit_idea的 alibaba cloud tookit下载-程序员宅基地
文章浏览阅读1w次。在没有jenkins环境下,特别是在快速更新版本的情况下,来回部署很花时间,所以博主找到了这个方法。注意:最好是简单的单应用部署首先,在IDEA插件库搜索Alibaba Cloud Toolkit,如下图,安装完成后重启IDEA即可用如果在内网环境下,先下载【离线包】确保 IntelliJ 版本 2018.2.* 及以上http://toolkit.aliyun.com/i..._idea的 alibaba cloud tookit下载
Spark操作mysql-程序员宅基地
文章浏览阅读56次。2019独角兽企业重金招聘Python工程师标准>>> ..._spark执行mysql语句
高光谱图像分类--HybridSN: Exploring 3-D–2-DCNN Feature Hierarchy for Hyperspectral Image Classification_hybridsn: exploring 3-d–2-d cnn feature hierarchy -程序员宅基地
文章浏览阅读2.7k次。《HybridSN: Exploring 3-D–2-DCNN Feature Hierarchy for Hyperspectral Image Classification》S. K. Roy, G. Krishna, S. R. Dubey, B. B. Chaudhuri HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification, IEEE GRSL 2020这篇论文构建了一个_hybridsn: exploring 3-d–2-d cnn feature hierarchy for hyperspectral image c
ftp 报错 553 Could not create file_553 could not create file.-程序员宅基地
文章浏览阅读1.3w次,点赞9次,收藏15次。在使用 ftp put 命令进行文件上传时报错。ftp 报错 553 Could not create file_553 could not create file.